Teams勉強会
昨年末、ほしぞloveログのSamさんの呼びかけで、Teams上の画像処理座談会が行われたことがありました。テーマは「デジカメのノイズ」。もともとSamさんはノイズの専門家だそうですし参加者にはあぷらなーと氏、天リフの編集長、タカsiさん、Kagayaさん、kさんなど有名な方々だけでなく、有名会社でデジカメのセンサーを開発されている方とかが集まって相当にインパクトが強い「学会」でした。
この「学会」は一回限り。それではもったいないということで、ダボさん (関東で大学院生していて、天体写真をテーマにした研究をされている)の呼びかけて小さな画像処理研究会が組織されました。月に一回、満月の頃にTeamsのミーティングをやっています。
今月、その3回目のミーティングがありました。テーマは"deconvolution"。プレゼンターはブログ
を管理されているkさんです。お分かりの方なら「おお!」と思われたのではないでしょうか?21cmのニュートンと決して最新型ではない冷却CCDの組み合わせで、けっこうマイナーな銀河をしかも光害地から撮影されています。その画像はすさまじく、天文ガイドの入選もほぼ毎月という方です。最優秀賞も複数回受賞されているのではないでしょうか(確認してませんが)。
そのkさんが、銀河の"deconvolution"について話してくださるというのですから、顧問は3日くらい前から興奮していました。しかも私とそーなのかー氏が合作で撮影したNGC2903を例に処理の仕方やマスクの掛け方を話していただけました。
ちなみに下の写真が、私が一生懸命に処理したNGC2903です。

同じソースを使って、kさんが処理をおこなうと次のようになります。

・・・(無言
今回のエントリは、ミーティング得た内容をもとにして、上のイマイチなNGC2903を再処理した過程について、紹介したいと思います。
そもそもDeconvolutionとは
もし究極の望遠鏡とカメラがあったとしたら、それで撮影した星は1ピクセルの点として記録されるはずです。そのとき星雲や銀河はどんな姿なのか想像するだけでヨダレがでそうです。実際の天体写真では、星はぼんやりした楕円に写っています

こんな感じです。しかし,この星像には
「理想的には1ピクセルの点であるはずの星が、光学系と大気の揺らぎでどれだけぼやけるか?」
という貴重な情報が含まれているわけです。画像上での座標をとすれば,ボヤけた星を平均した輝度の分布は2変数の関数
で表すことができます。これはPSF(Point Spread Function)と呼ばれていて、にある点光源の星が
の位置にどれだけの輝度を与えるか?つまり画像のボケ具合を表しています。
さて、究極のレンズとカメラがないと撮影できない「真の」天体像の輝度の分布を仮にとし、顧問の普通のカメラとレンズで撮影した「ぼやけた」天体像の輝度の分布を
とします。それらの間には余計なノイズなどを度外視すれば
という関係があります(この右辺は畳み込み(convolution)積分と名前がついています)。は画像の大きさを表しています。
いまと
がわかっているので、原理的にはこの式を逆に辿れば
をもとめることができるはず、というのが"deconvolution(逆たたみこみ)"の考え方です。PSF関数を星の画像そのものから得られるこの方法は,天体写真にとって最適なシャープ化の手法といえるかもしれません。
(1)式からを解く方法はいくつか提案されていて、中でも"Regularrized Richardson-Lucy" というのがその標準的な手法のようです。たとえば
の解説が比較的わかりやすいです。顧問も完全には理解できていないのですが、要は反復法とよばれる逐次近似計算によって、適当に仮定した近似解を,漸近的に本当の解へ収束させることをおこなっているようです。
Pixinsightでの操作法、パラメターの意味
Pixinsightには"deconvolution"の機能が搭載されています。
まず"Dynamic PSF"という機能で星の平均値からPSF関数を作った後,それを"deconvolution"に渡して計算を行います。その手続きはおなじみNiwaさんのブログ
にわかりやすく説明されていますので,ご覧ください。
いかではそのときに設定するパラメータの意味を考えてみます。下はDeconvolutionのウインドウです。右上の小さなウインドウは"Dynamic PSF"で得られた星像。ウインドウの最上段"PSF"のタブのところで,この星像を指定しています:
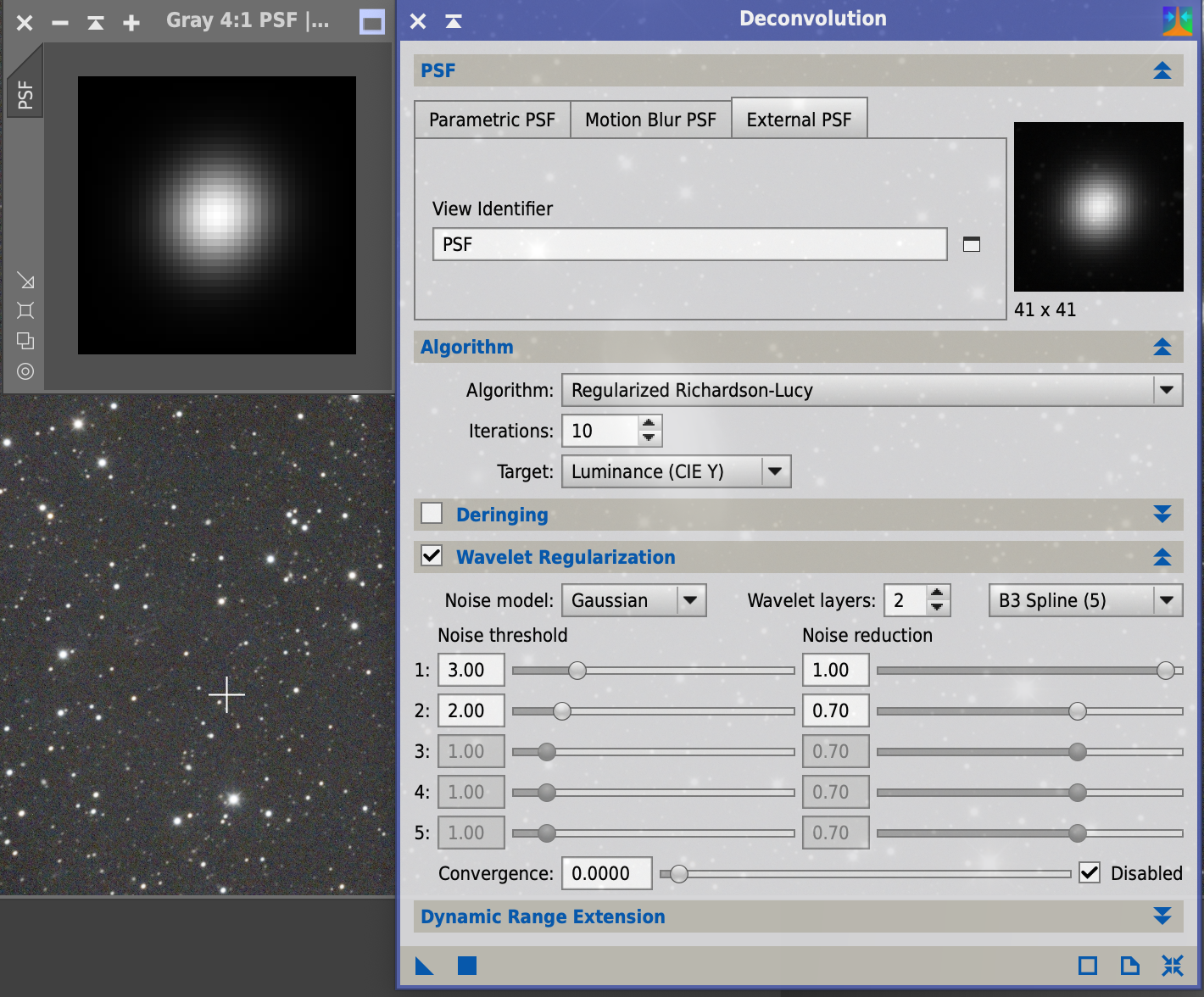
次に2段目の"Algorithm"です。
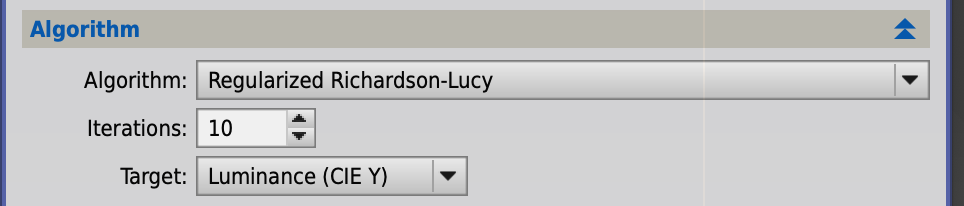
1行目では,(1)式を解くための複数の手法のうちいづれか(ここでは標準的なRichardson-Lucyを選んでます)を指定しています。つぎの"Iteration"は、上記の反復計算の回数ですね。基本的にはたくさん繰り返せばより真のへ画像が近づいていくはずですが、画像にノイズなどが含まれていると、繰り返しを増やしすぎることによって、そのノイズが増幅されてしまったり、または数値振動を起こしたりと不具合も起こります(ちなみにkさんは100回を基本にしているとのことでした)。具体的な値は元画像との相談になるようですが,20~30回くらいがよいようです。
次に重要なのが、3段目の"Deringing"の設定です。どうしても生じてしまう星の周りに位落ち込みが生じるのを防ぐのが目的です。
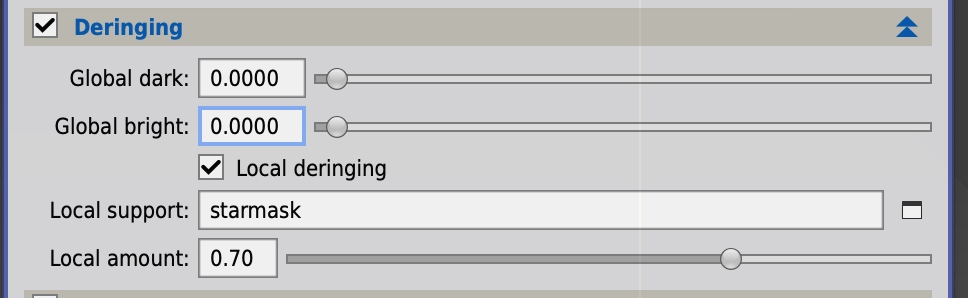
local supportに星マスクを与えて、Local amountでその強度を調整するというのはNiwaさんのブログにあるとおりです。
Global BrightとGlobal Darkは、Deconvolution処理による輝度の修正の上限値と下限値を与えているもと思われます(これはちゃんとしたソースを見つけることができておらず、顧問の推測です)。つまりGlobal Dark=0.01とした場合、Deconvolutionの解の輝度が0.01以下になるとしたら、そこで強制カットオフして輝度を0.01以下にならないようにしていると予想しています。
kさんは、このGlobal Darkを基本的には0とし、最大限暗部を強調する手法をとられているようです。代償として生じるリンギングはマスク処理によって徹底的に排除されているようでした。書籍Inside Pixinsightや、Light Vortex Astronomy をみてもGlobal Darkを有限の値で調整してリンギングを防ぐと書いてあるので、これを0にしてしまう発想はありませんでした。ここが重要です。
NGC2903の再処理
ここからはあっさりめに行きます。上記の方針でDeconvolutionをやってみましょう。下は、スタック後にカラーバランスだけ調整して仮ストレッチしたものです。

これに対して、適当にPSFを作った後とくにマスク処理せずにIteration=50, GlobalDark=0としてDeconvolutionをかけてみます。するとこんな感じ

銀河中心部の解像”感”は劇的に上がっています。驚くほどです。これ、Global Darkを有限にしてしまうと、とくに暗黒帯のディーテールが浮かび上がってきません。ですが星の周りは強烈なリング、背景部分もモヤモヤとしたアーティファクトが浮かんでしまいます。これはマスクで防ぐことになるわけです。
Pixinsightでマスク作るのって簡単でないんですが、がんばって下のようなものをこさえました
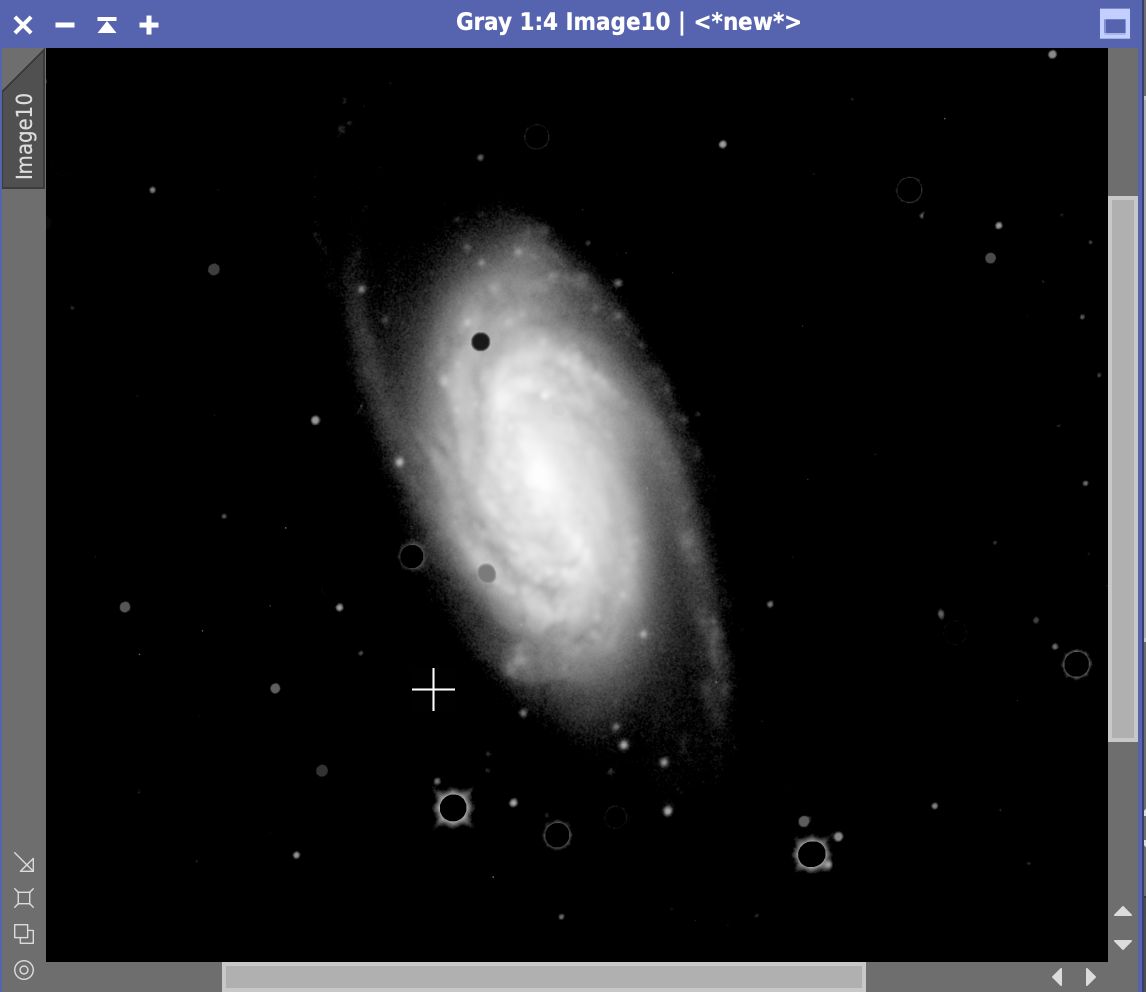
銀河の中心部だけを選択し、中の微光星は黒抜きで保護します。これを適当にボカしながら元画像に適用し、再度Deconvolutionを行いました。
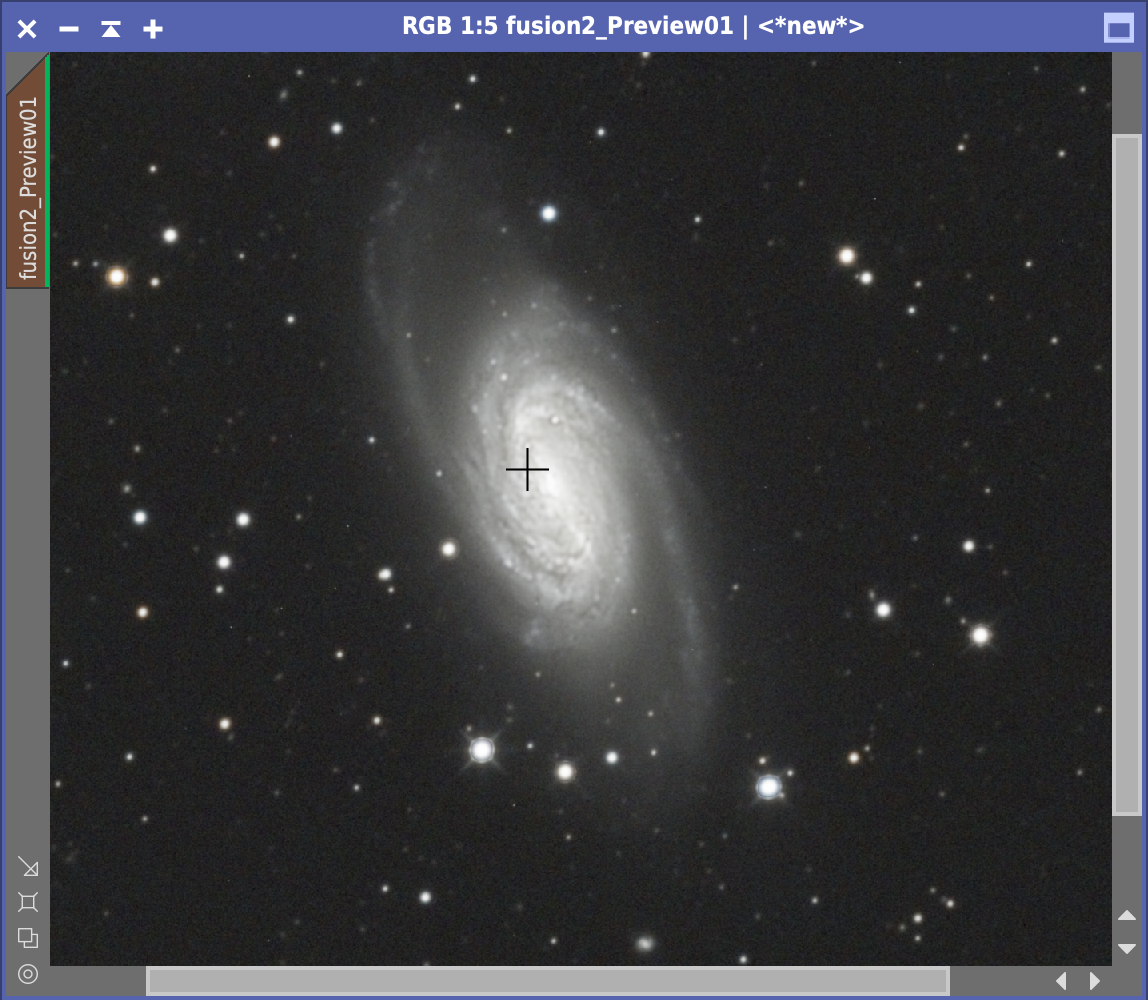
大体良さそうです。もう一度元画像と比べてみます。
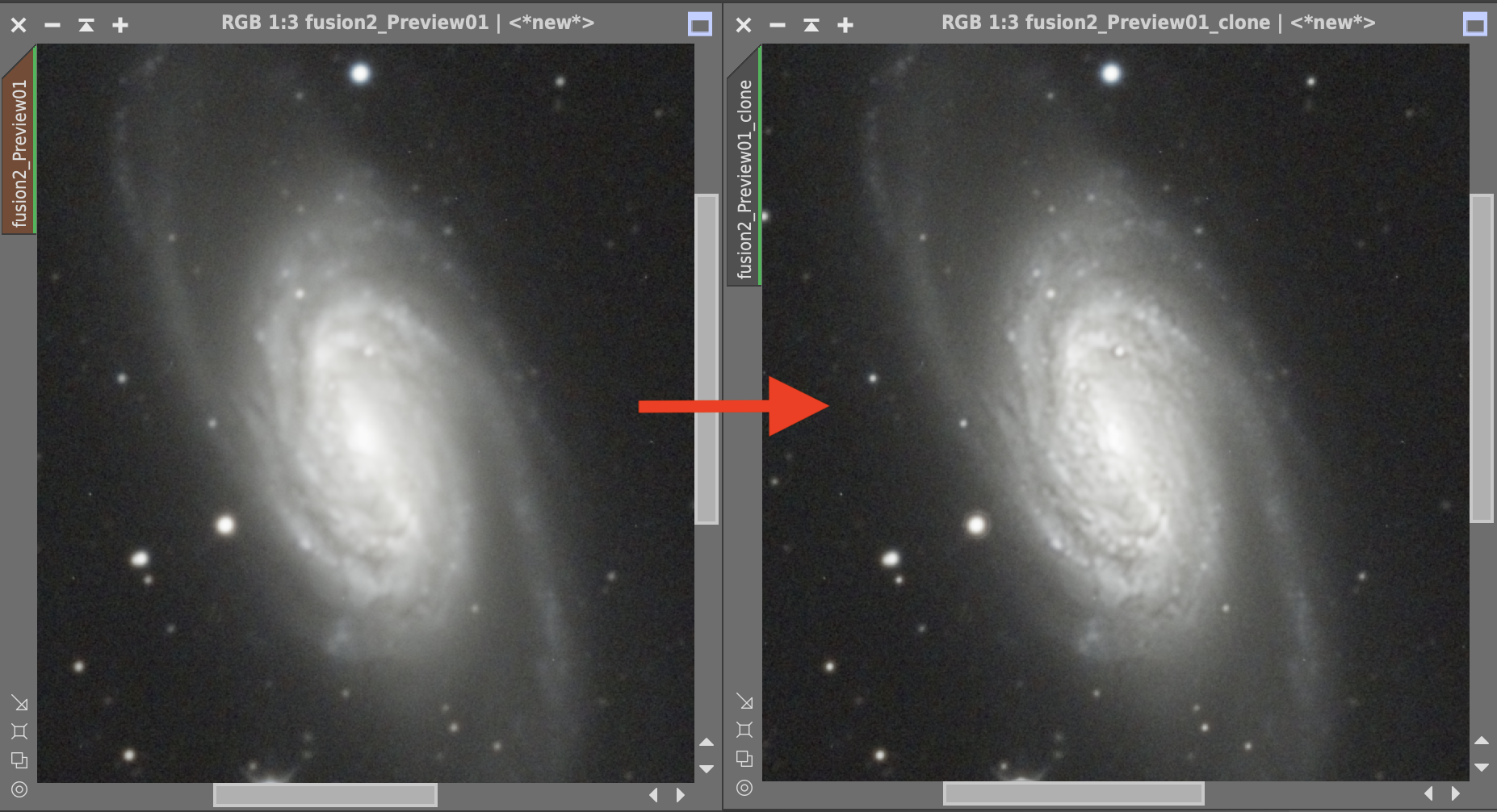
細かく見ると、周辺の星像がまだ変になっているので、その辺はもっとマスクの精度を上げる必要がありそうです。もうちょっと修行が必要ということで、今回はこのへんにしたいと思います。疲れた。